Комплексные числа
В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ \mathbb{C} $.
Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = \sqrt{-1} $, числа $ a,b \in \mathbb{R} $ вещественные.
Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ \mathbb{R} \subset \mathbb{C} $. К слову говоря также возможно, что $ a = 0 $.
Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.
Введем понятие комплексно-сопряженных чисел. К каждому комплексному числу $ z = a+ib $ существует такое, что $ \overline{z} = a-ib $, которое и называется сопряженным. Такие числа отличаются друг от друга только знаками между действительной и мнимой частью.
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
- Алгебраическая $ z = a+ib $
- Показательная $ z = |z|e^{i\varphi} $
- Тригонометрическая $ z = |z|\cdot(\cos(\varphi)+i\sin(\varphi)) $
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
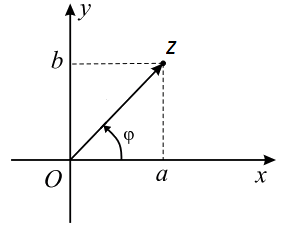Видим, что $ a,b \in \mathbb{R} $ расположены на соответствующих осях плоскости.
Комплексное число $ z = a+ib $ представляется в виде вектора $ \overline{z} $.
Аргумент обозначается $ \varphi $.
Модуль $ |z| $ равняется длине вектора $ \overline{z} $ и находится по формуле $ |z| = \sqrt{a^2+b^2} $
Аргумент комплексного числа $ \varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.
Если:
- $ a>0 $, то $ \varphi = arctg\frac{b}{a} $
- $ a<0, b>0 $, то $ \varphi = \pi + arctg\frac{b}{a} $
- $ a<0, b<0 $, то $ \varphi = -\pi + arctg\frac{b}{a} $
Операции
Над комплексными числами можно проводить различные операции, а именно:
- Складывать и вычитать
- Умножать и делить
- Извлекать корни и возводить в степень
- Переводить из одной формы в другую
Для нахождения суммы и разности складывается и вычитаются только соответствующие друг другу члены. Мнимая часть только с мнимой, а действительная только с действительной:
$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$
$$ z_1 - z_2 = (a_1+ib_1) - (a_2+ib_2) = (a_1 - a_2)+i(b_1 - b_2) $$
Умножение в алгебраической форме:
$$ z_1 \cdot z_2 = (a_1+ib_1) \cdot (a_2+ib_2) = (a_1 a_2 - b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$
Умножение в показательной форме:
$$ z_1 \cdot z_2 = |z_1|e^{i\varphi_1} \cdot |z_2|e^{i\varphi_2} = |z_1|\cdot|z_2|\cdot e^{i(\varphi_1 + \varphi_2)} $$
Деление в алгебраической форме:
$$ \frac{z_1}{z_2} = \frac{a_1+ib_1}{a_2+ib_2} = \frac{a_1 a_2 + b_1 b_2 }{a_2 ^2 + b_2 ^2} + i \frac{a_2 b_1 - a_1 b_2}{a_2 ^2 + b_2 ^2} $$
Деление в показательной форме:
$$ \frac{z_1}{z_2} = \frac{|z_1|e^{i\varphi_1}}{|z_2|e^{i\varphi_2}} = \frac{|z_1|}{|z_2|}e^{i(\varphi_1 - \varphi_2)} $$
Для возведения в степень необходимо умножить комплексное число само на себя необходимое количество раз, либо воспользоваться формулой Муавра:
$$ z^n = |z|^n(\cos n\varphi+i\sin n\varphi) $$
Для извлечения корней необходимо также воспользоваться формулой Муавра:
$$ z^\frac{1}{n} = |z|^\frac{1}{n}\bigg(\cos \frac{\varphi + 2\pi k}{n}+i\sin \frac{\varphi + 2\pi k}{n}\bigg), k=0,1,...,n-1 $$
Так же теория комплексных чисел помогает находить корни многочленов. Например, в квадратном уравнении, если $ D<0 $, то вещественных корней нет, но есть комплексные. В последнем примере рассмотрен данный случай.
Рассмотрим на практике комплексные числа: примеры с решением.
Примеры с решением
| Пример 1 |
| Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$ |
| Решение |
|
Для начала приступим к нахождению модуля комплексного числа: $$ |z| = \sqrt{4^2 + (-4)^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2} $$ Осталось найти аргумент: $$ \varphi = arctg \frac{b}{a} = arctg \frac{-4}{4} = arctg (-1) = -\frac{\pi}{4} $$ Теперь составляем тригонометрическую запись комплексного числа, указанного в условии примера: $$ z = 4\sqrt{2}\bigg(\sin(-\frac{\pi}{4}) + i\sin(-\frac{\pi}{4}) \bigg) $$ Тут же можно записать показательную форму: $$ z = 4\sqrt{2} e^{-\frac{\pi}{4}i} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ z = 4\sqrt{2}\bigg(\sin(-\frac{\pi}{4}) + i\sin(-\frac{\pi}{4}) \bigg) $$ $$ z = 4\sqrt{2} e^{-\frac{\pi}{4}i} $$ |
| Пример 2 |
|
Вычислить сумму и разность заданных комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$ |
| Решение |
|
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел: $$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 - i $$ Аналогично выполним вычитание чисел: $$ z_1 - z_2 = (3+i) - (5-2i) = (3-5)+(i+2i) = -2 + 3i $$ |
| Ответ |
| $$ z_1 + z_2 = 8 - i; z_1 - z_2 = -2 + 3i $$ |
| Пример 3 |
|
Выполнить умножение и деление комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$ |
| Решение |
|
$$ z_1 \cdot z_2 = (3+i) \cdot (5-2i) = $$ Просто на просто раскроем скобки и произведем приведение подобных слагаемых, так же учтем, что $ i^2 = -1 $: $$ = 15 - 6i + 5i -2i^2 = 15 - i - 2\cdot(-1) = $$ $$ = 15 - i + 2 = 17 - i $$ Так, теперь разделим первое число на второе: $$ \frac{z_1}{z_2} = \frac{3+i}{5-2i} = $$ Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки: $$ = \frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = \frac{15 + 6i + 5i + 2i^2}{25 + 10i - 10i -4i^2} = $$ $$ = \frac{15 + 11i -2}{25 + 4} = \frac{13 + 11i}{29} $$ Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы: $$ \frac{z_1}{z_2} = \frac{13}{29} + \frac{11}{29}i $$ |
| Ответ |
| $$ z_1 \cdot z_2 = 17 - i; \frac{z_1}{z_2} = \frac{13}{29} + \frac{11}{29}i $$ |
| Пример 4 |
| Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $ |
| Решение |
|
1) $ n = 2 $ Для возведения в квадрат достаточно умножить число само на себя: $$ z^2 = (3+3i)^2 = (3+3i)\cdot (3+3i) = $$ Пользуемся формулой для умножения, раскрываем скобки и приводим подобные: $$ =9 + 9i + 3i\cdot 3 + 9i^2 = 9 + 18i - 9 = 18i $$ Получили ответ, что $$ z^2 = (3+i)^2 = 18i $$ 2) $ n = 7 $ В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую. Вычисляем значение модуля: $$ |z| = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} $$ Найдем чем равен аргумент: $$ \varphi = arctg \frac{3}{3} = arctg(1) = \frac{\pi}{4} $$ Записываем в тригонометрическом виде: $$ z = 3\sqrt{2}(\cos \frac{\pi}{4} + i\sin \frac{\pi}{4}) $$ Возводим в степень $ n = 7 $: $$ z^7 = (3\sqrt{2})^7 (\cos \frac{7\pi}{4} + i\sin \frac{7\pi}{4}) = $$ Преобразуем в алгебраическую форму для наглядности: $$ =(3\sqrt{2})^7 (\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}) = $$ $$ = 3^7 \sqrt{2}^7 (\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}) = $$ $$ = 3^7 \sqrt{2}^6 (1-i) = 3^7 \cdot 8(1-i) = $$ $$ = 2187 \cdot 8 (1-i) = 17496(1-i) $$ |
| Ответ |
|
$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$ |
| Пример 5 |
| Извлечь корень $ \sqrt[3]{-1} $ над множеством $ \mathbb{C} $ |
| Решение |
|
Представим число в тригонометрической форме. Найдем модуль и аргумент: $$ |z| = \sqrt{(-1)^2 + 0^2} = \sqrt{1+0} = \sqrt{1}=1 $$ $$ \varphi = arctg \frac{0}{-1} +\pi = arctg 0 + \pi = \pi $$ Получаем: $$ z = (\cos \pi + i\sin \pi) $$ Используем знакомую формулу Муавра для вычисления корней любой степени: $$ z^\frac{1}{n} = r^\frac{1}{n}\bigg(\cos \frac{\varphi + 2\pi k}{n}+i\sin \frac{\varphi + 2\pi k}{n}\bigg), k=0,1,...,n-1 $$ Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $: $$ z_0 = \sqrt[3]{1} (\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}) = \frac{1}{2}+i\frac{\sqrt{3}}{2} $$ $$ z_1 = \sqrt[3]{1} (\cos \frac{3\pi}{3}+i\sin \frac{3\pi}{3}) = -1 $$ $$ z_2 = \sqrt[3]{1} (\cos \frac{5\pi}{3}+i\sin \frac{5\pi}{3}) = \frac{1}{2} - i\frac{\sqrt{3}}{2} $$ |
| Ответ |
|
$$ z_0 = \frac{1}{2}+i\frac{\sqrt{3}}{2} $$ $$ z_1 = -1 $$ $$ z_2 = \frac{1}{2} - i\frac{\sqrt{3}}{2} $$ |
| Пример 6 |
| Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ \mathbb{C} $ |
| Решение |
|
Решать будем по общей формуле, которую все выучили в 8 классе. Находим дискриминант $$ D = b^2 - 4ac = 2^2 - 4\cdot 1 \cdot 2 = 4-8 = -4 $$ Получили, что $ D=-4<0 $ и казалось бы, что решение можно заканчивать. Но нет! В нашем задании требуется решить уравнение над комплексным множеством, а то что дискриминант отрицательный означает только лишь отсутствие вещественных корней. А комплексные корни есть! Найдем их продолжив решение: $$ x_{1,2} = \frac{-b\pm \sqrt{D}}{2a} = \frac{-2\pm \sqrt{-4}}{2} = $$ Заметим, что $ \sqrt{-4} = 2\sqrt{-1} = 2i $ и продолжим вычисление: $$ = \frac{-2 \pm 2i}{2} = -1 \pm i $$ Получили комплексно-сопряженные корни: $$ x_1 = -1 - i; x_2 = -1 - i $$ Как видите любой многочлен можно решить благодаря комплексным числам. |
| Ответ |
| $$ x_1 = -1 - i; x_2 = -1 - i $$ |
В статье "Комплексные числа: примеры с решением" было дано определение, основные понятия, формы записи, алгебраические операции и решение практических примеров.
Нужно подробное решение своей задачи?
ЗАКАЗАТЬ РЕШЕНИЕ